Viscosity

Newton's Law

Newton defines the coefficient of viscosity from the equation F = Ah(dv/dx) . This gives the force F between two adjacent slabs of fluid of contact area A and thickness dx that are sliding over each other with a relative velocity dv. (dv/dx) is called the velocity gradient.

Rearranging this formula gives h = F /A(dv/dx). If you think about it, the right hand side of this expression has the form

Substituting for force, area and speed gives

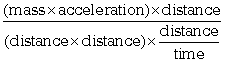
which simplifies to

Now if we substitute for acceleration we obtain

which simplifies, finally to

which we abbreviate to [M] [L]^-1 [T]^-1. So if we want a unit for the coefficient of viscosity, we will use kg m^-1 s^-1, sometimes simply called a Poise.  [M] encapsulates the idea of 'massness' which is what kilograms, ounces, hundredweights, etc all have in common. It is called the 'dimension' of mass. Similarly [L] and [T] are the dimensions of length and time.

If you write an equation, the units must come out the same on both sides. We formalise this in the Method of Dimensions by requiring that the powers to which [M], [L] and [T] appear must be the same on each side of the equation.

Stokes' Law

Consider a sphere of radius a falling through a fluid with a velocity v (which may or may not be terminal). Suppose that the force is given by F = k v^xa^yh^z. (the size of the object is conventionally written as a. In the case of a sphere, a=r.) Write the dimensional version of this and hence find x, y and z.  Here is the solution.

Drag Force

Newton's defining equation has slabs of fluid sliding over one another like spreading a pack of cards. This is called streamline flow, and if you don't have flow like this you can't use the notion of viscosity at all, because the coefficient would be undefined. You might then want to consider the density of the fluid.

So, suppose that the force is given by F = k v^xa^yr^z.  Write the dimensional version of this and hence find x, y and z. If you remember that the cross-sectional area of the falling body is proportional to a², you may find that you recognise the result. Here is the solution.

Reynolds' Number

There is a dimensionless number that determines whether the flow is likely to be streamline or turbulent. The variables in its formula are the coefficient of viscosity, the density, a variable dependent on the size of the system and the velocity of the fluid. Try using the Method of Dimensions to discover the form of the equation for Reynolds' Number. There is an obvious problem in that you have four variables (x, y, z and, say, w). You need to reflect on the dimensionless aspect of the problem. The solution is here.