1

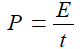
Energy Methods

You need at your fingertips the following formulae

kinetic energy	E_kinetic = ½mv²	m = mass, v = velocity
(gravitational) potential energy (change)	E_{gravitational} = mgΔh	m = mass, h = height (change), g = gravitational field strength (= 9.8 N/kg)
elastic (potential) energy		λ = modulus of elasticity, l = unstretched length, x = extension (= current length - l )
work done against a force (often resistive or frictional, but not always)	E_work = Fs E_work(= F.s = Fs cosθ)	F = force, s = distance moved, using the component along the line of the force. The the vector formulation is not often needed.
power		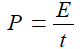E can stand for any form of energy
power	P = F v	F = force, P = power, v = velocity

In all of these formulae, you must use a consistent system of units (metres, kilograms, seconds, joules, etc.)

Identify all the forms of energy present at the start of the question
Identify all the forms of energy present at the end of the question
Write expressions for all the energy changes by subtracting the final energy of any given type from the initial energy of that type
Write an equation of the form

Sum of energy changes = 0

Substitute formulae from the table above
Solve for the unknown.

Worked example

A skier sets off down a slope with a starting velocity of 5 m/s. The slope is 500 m long and involves a drop in height of 200 m. During the run, there is a total resistive force of one tenth of the skier's weight. Calculate the velocity at the bottom of the run.

Notice that we are not given the mass of the skier, and yet it appears in most of the energy formulae. With any luck it will cancel out, so we put it in as m whenever we need to and keep our fingers crossed.

KE at start = ½m × 5² = 12.5m
KE at finish = ½mv²
GPE change = m × 9.8 × 200 = 1960 m
Work done against resistive forces = (mg/10) × 500 = 490 m

We have to be a little careful about the sign of the various energy changes:

The skier gets faster, so we have more KE at the end: the change is positive.
The skier falls to a lower level, so we have less GPE at the end: the change is negative.
The work done against friction ends up melting some snow, so we have more thermal energy at the end: the change is positive

ΔKE + ΔGPE + Δwork = 0	The signs are all positive at this stage because this is just the standard equation
(½mv² - 2.5m) - 1960 m + 490 m = 0	Signs have become negative where our logic has told us that the value we are substituting is negative
½v² = 1472.5	Cancelling by m and re-arranging
v = 54 m/s	This is quite fast - about 100 mph.