Year 12
Homework hints
This technique is for splitting a matrix up into its constituent parts: a stretch matrix and a reflection/rotation matrix (just one or the other of these). It will only work if the leading diagonal elements are in the same ratio (ignoring signs) as the off-diagonal elements. If this condition is not satisfied then the matrix in question cannot be de-constructed, and doesn't represent a combined transformation in the first place. (If one of the ratios is 0/0, that counts as equal to the other ratio.) You need to be familiar with the pages on the various types of transformation matrix.
Let's proceed, by example, to reverse engineer this matrix:
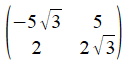
The ratio in question is 5:2, so we will begin by writing (as a first shot) the relevant stretch matrix as
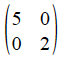
and writing our 'residual' matrix as the original with the top row divded by 5 and the bottom row divided by 2, thus:
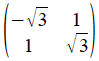
The 'residual' matrix has the structure of a reflection matrix, but it isn't quite right yet, as the elements are too big to represent cos() or sin(). So we must evaluate
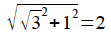
Now we multiply everything in our putative stretch matrix by 2 and divide everything in the 'residual' matrix by 2, thus
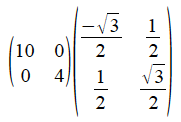
Check you agree that the product of these two matrices is indeed the matrix we started with.
The second of them we recognise (or find with a calculator!) as
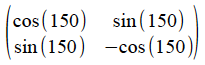
which represents a reflection in a line inclined at 75º to the x-axis (75 being half of 150).
The first we recognise as a matrix with an x-stretch factor of 10 and a y-stretch factor of 4