M2
hints - Jan 2007
First, read the page on Energy Methods.
Part (a) of this question is almost identical to the worked example, except that there is no resistance force term to worry about, and the initial kinetic energy is zero.
Part (b) is even more similar to the worked example. Again there is no initial kinetic energy but, in this case, we know the final kinetic energy, but not the frictional force.
Copy the diagram, but without the chains (the thick black lines). In their stead put vertical lines with an open-headed force arrow, like the one shown on the right, and label them TA and TB. Draw a downward open-headed force arrow that starts in the centre of the rectangle, labelling it W.
Remember that the moment of a force is defined as r×F. For the purposes of this question, you may forget about the cross product aspect, and just use r F, so long as you remember that r has to be the perpendicular distance from the fulcrum (pivot) to the force arrow, extended with a dotted line if need be.
For the purposes of taking moments, you are entitled to choose any point you like as the fulcrum. If you choose a point lying on one of the force arrows (extended if necessary), then the perpendicular distance of the pivot from that force is obviously zero, which means that the force in question will make no contribution to the moments equation.
The moments equation to use here is
anticlockwise moment = clockwise moment.
Begin by choosing a pivot at A, so that the only forces contributing are TB and W. The perpendicular distance of TB from the fulcrum can be read directly from the diagram, while the perpendicular distance of W from the fulcrum is just half the overall width of the rectangle.
First, read the page on Energy Methods. The equation to use is very simply
KE gained = GPE lost
Even if you haven't managed to do part (a), you can still use its result as a starting point for (b). Draw a blob to represent the particle, drawing an upward force arrow labelled T and a downwawrd force arrow labelled mg. By the side of this diagram draw a second blob labelled m, and attach to it an acceleration arrow, like the one shown on the right, labelled a.
Now use the equation
Fresultant = ma
In this case, the resultant force upward is (T - mg), while the acceleration upward is v2/r
Draw in the diagonals of the top rectangle, AB and HC. Where they interset - lets call it M - is the centre of mass of the top rectangle, and you can easily see how far it is from AB. Do the same for the bottom rectangle, calling the intersection of the diagonals N.
Next find the areas of the two rectangles. It is sometimes useful to use the concept of a superficial density (the mass of a unit area rather than a unit volume). Let's denote the superficial density by the lower-case greek sigma σ. If you multiply this in turn by the two areas, you will obtain the masses of the two rectangles, and hence be in a position to write down their weights.
Draw a line PQ straight down the middle of the T-shape - it will go through the two intersections of diagonals. P is where this line meets AB and Q is where it meets FE
Now draw a side view of the shape, looked at from the left-hand side of the page. You should have drawn a straight line with P at its left-hand end and Q at the right-hand end. Mark blobs on this line to show the position of the two centres of mass M and N - one should be half-way between P and (HGDC), and the other half-way between (HGDC) and F. Add vertical force arrows to the blobs, and label them with the respective weights.
There must be a place, somewhere between the two blobs - let's call it Z - such that the blob on its left causes an anticlockwise moment that is exactly equal to the clockwise moment caused by the blob on its right. Z is then called the centre of mass of the whole object. Let x be the distance from P to Z. Because you know how far the blobs M and N are from P, you can express the distances MZ and NZ in terms of x.
You are now in a position to write an equation expressing the equality of the anticlockwise and clockwise moments about Z, and hence to find x.
For part (c) you need to realise that, when the shape is hung from X, it will swing until the overall centre of mass Z hangs vertically below X. Since you now know where on the diagram to place Z, you can draw the line XZ and find the angle it makes with AB by normal trigonometry.
Part (a) is a matter of knowing what sin and cos are for 0 and 2π. For part (a)(iii) you should notice that when Tom is vertically below his starting point, his displacements in the i and j directions are the same as they were at t = 0. I'd be inclined to sketch the cosine and sine curves, go up from t = 0 to the curves, and then draw horizontal lines to the right, noting the first two occasions where both lines meet their curve (remember the trig stuff in FP1).
To find a velocity, you differentiate the position vector r with respect to t. Differentiating 'with respect to' t means that you apply the differentiation rules to functions of t but not to functions of anything else - so you'd leave x2 as x2, for example, whereas you would change t3 to 3t2 , change cos(t) to -sin(t), and eliminate completely any term that contains no t at all.
To find an acceleration, you differentiate the velocity with respect to t. Then multiply by the mass to find the force. Finally find the magnitude of the force in the usual way, by finding the dot product of the force vector with itself and square rooting.
Each revolution is 2π radians, so that enables you to work out how many radians there are per minute and hence per second. This is called the angular velocity, and is denoted by the greek letter ω (omega). It is related to the linear (ordinary) velocity by v = ω r. So far as centripetal acceleration is concerned, it may be expressed as either v²/r or as ω² r.
Begin (c) by drawing a blob and attaching to it a sloping force arrow labelled T and a vertical force arrow labelled mg. Write, "Resolving vertically, there is no vertical acceleration, so the upward and downward components of force are equal". Then write an equation which has the downwarde force on one side and the appropriate component of T on the other.
For (iii), write, "Resolving horizontally, the horizontal component of T provides the centripetal mass-acceleration". Then write an equation with the horizontal component of T on one side and m ω² r on the other. Use your answer to (ii) to substitute for T, and you should be home and dry.
You have to know for this question that
power = force × velocity P = F v
(and to remember, when using it, that 1 kW = 1000 W). [You can easily satisfy yourself that this formula is OK by dividing both sides of the work done formula by time.] If you plug the formula for force given in the question into the formula, and set it equal to 72 kW, the answer should drop out easily enough.
For part (b), they have given you a formula for resistive force (which is negative), so you divide by mass to find the acceleration, and then remember that acceleration is dv/dt.
For part (ii), you need to integrate the equation of (i). The particular differentiation/integration trick you need for this is

The double-headed arrow is a two-way 'implies that' sign. You will notice that the equation you are trying to integrate is just like dy/dx = ky, except that the y has been written as v, the x as t and the k as -(1/25). It is the structure of the equation that matters, not the shapes of the individual letters used. So you should be able to write down the equation corresponding to y = ex.
But you must remember to include + c on the right-hand side as the arbitrary constant of integration. To deal with this, you need the so-called 'boundary condition' that when t = 0, v = 20 (as you are told in the question). Plugging these values in, and remembering that anything to the power 0 is 1, will enable you to find c.
This question needs the spring equation
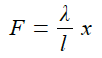
In equilibrium, the up and down forces are equal: the up force is the elastic force, given by the formula above, while the down force is just the weight, given by mg. For (b), refer to the third line of the table on the Energy Methods page.
At the beginning of (c), the block has no kinetic energy, and it has none at the end either, when it has come to rest again. Use the Energy Methods technique, bearing in mind that the Elastic Energy formula works just as well for compressions as for extensions.